Bài toán: Số nguyên tố

Tý là một cậu bé rất thích học môn Toán, cậu thường xuyên tìm hiểu, nghiên cứu và giải các bài toán khó. Trong giờ học Toán hôm nay, Tý tìm hiểu về số nguyên tố. Sau khi tìm hiểu khái niệm về số nguyên tố, Thầy giáo có giao cho Tý một bài tập cũng liên quan về số nguyên tố, cụ thể như sau:

Đề bài: Cho trước một số nguyên dương ~N~, hãy ghi ra kết quả số lượng các số nguyên tố nhỏ hơn hoặc bằng ~N~.

Dữ liệu vào:

• Đọc một số nguyên dương ~N~ ~(0 < N \leq 10^6)~.

Dữ liệu ra:

• Ghi ra một số ~K~ là số lượng số nguyên tố thoả mãn đề bài.

Ví dụ:

Input

10

Output

4

Giải thích:

• Các số nguyên tố ~\leq 10~ là: ~2, 3, 5, 7~. Vậy có ~4~ số.

Giới hạn:

• Subtask 1: Có ~30\%~ số test ứng với ~0 < N \leq 1000~.
• Subtask 2: Có ~70\%~ số test ứng với ~0 < N \leq 10^6~.

Bài toán: Robot quét nhà

Robot quét nhà đang ở điểm gốc tọa độ ~(0, 0)~ nhận được mỗi ký tự là một lệnh di chuyển với quãng đường bằng một đơn vị độ dài. Gồm các lệnh sau:

• Lệnh E: đi về hướng đông,
• Lệnh S: đi về hướng nam,
• Lệnh W: đi về hướng tây,
• Lệnh N: đi về hướng bắc.

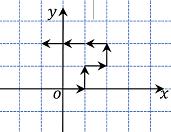
Trục ~Ox~ chỉ về tọa độ chạy từ tây sang đông,
Trục ~Oy~ chỉ về tọa độ chạy từ nam lên bắc.

Ví dụ:

Với dòng lệnh "ENENWWW", sau khi thực hiện robot sẽ tới vị trí ~(-1, 2)~.

Yêu cầu:

• Xác định tọa độ của robot sau khi thực hiện lệnh di chuyển nhận được.

Dữ liệu vào:

• Dòng một chứa một số nguyên ~T~ ~(T \leq 100)~ — số lệnh.
• ~T~ dòng tiếp theo, mỗi dòng chứa một xâu ký tự ~S~ chỉ gồm các ký tự "E", "W", "S" và "N", thể hiện một lệnh di chuyển của robot.

Kết quả:

• Ghi ra gồm ~T~ dòng, mỗi dòng tương ứng với tọa độ của robot sau khi thực hiện lệnh di chuyển nhận được.

Ví dụ:

Input

2
ENENWWW
EESSWNNN

Output

-1 2
1 1

Giải thích:

• Với lệnh "ENENWWW": Robot đi tới vị trí ~(-1, 2)~.
• Với lệnh "EESSWNNN": Robot đi tới vị trí ~(1, 1)~.

Giới hạn:

• Có ~60\%~ số test tương ứng ~40\%~ số điểm của bài với ~1 \leq T \leq 100, |S| \leq 1000~;
• Có ~40\%~ số test tương ứng ~60\%~ số điểm của bài với ~1 \leq T \leq 100, |S| \leq 100,000~.

Bài toán: Cặp số

Đề bài:

Cho dãy số nguyên ~a_1, a_2, \dots, a_n~ và một số nguyên ~S~. Hãy đếm xem có bao nhiêu cặp chỉ số ~(i, j)~ với ~i \neq j~ mà tổng của ~a_i + a_j = S~.

Input:

• Dòng thứ nhất chứa hai số nguyên ~n~ ~(n \leq 10^5)~ và ~S~ ~(|S| \leq 10^9)~.
• Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \dots, a_n~ ~(|a_i| \leq 10^9)~.

Output:

• Một số nguyên duy nhất là số lượng cặp chỉ số ~(i, j)~ thỏa mãn yêu cầu.

Sample Input:

10 7
5 2 5 3 4 3 1 6 4 0

Sample Output:

7

Diễn giải:

• Các cặp ~(i, j)~ thỏa mãn ~a[i] + a[j] = 7~ là:
  • ~(1, 7): 5 + 2 = 7~,
  • ~(3, 7): 5 + 2 = 7~,
  • ~(4, 6): 3 + 4 = 7~,
  • ~(5, 6): 4 + 3 = 7~,
  • ~(8, 9): 6 + 1 = 7~.
• Tổng số cặp: ~7~.

Bài toán được diễn giải lại như sau:

Bài toán: Chia bánh quy

Peter đến thăm nhà của hai chị em Anna và Maria và phát hiện rằng họ có rất nhiều bánh quy được phân bố vào các túi để lưu trữ. Vì có quá nhiều bánh quy, Peter quyết định rằng sẽ chẳng có gì to tát nếu anh ấy lấy trộm một vài túi bánh. Tuy nhiên, anh ấy muốn đảm bảo rằng Anna và Maria sẽ không cãi nhau vì những chiếc bánh này.

Để tránh xảy ra tranh chấp, Peter chỉ muốn lấy đi một số túi bánh quy sao cho tổng số bánh quy còn lại trong các túi có thể chia đều thành hai phần (số bánh còn lại là một số chẵn). Hãy tính xem có bao nhiêu cách chọn túi để đảm bảo điều kiện này.

Dữ liệu vào:

1. Dòng đầu tiên chứa số nguyên N ~(1 \leq N \leq 10^6)~ — số lượng túi bánh quy mà Anna và Maria có.
2. Dòng thứ hai chứa N số nguyên dương ~A_1, A_2, ..., A_N~ ~(1 \leq A_i \leq 10^6)~ — số lượng bánh quy trong từng túi.

Dữ liệu ra:

• Một số nguyên ~K~ — là số cách chọn túi bánh sao cho tổng số bánh còn lại trong các túi là một số chẵn. Nếu không có cách nào thì in ra ~0~.

Ví dụ:

Input

1
1

Output

1

Input

2
1 1

Output

0

Input

10
1 2 2 3 4 4 4 2 2 2

Output

8

Giới hạn:

• ~40\%~ số test với ~1 \leq N \leq 1000~.
• ~60\%~ số test với ~1 \leq N \leq 10^6~.