Phát biểu bài toán

An cần đi từ nhà mình (nút giao thông ~ 1 ~) đến trường học (nút giao thông ~ n ~) bằng xe buýt. Thành phố có ~ n ~ nút giao thông và ~ m ~ tuyến xe buýt hai chiều, mỗi tuyến có giá vé ~ t_{ij} ~. An có một vé xe buýt miễn phí, cho phép đi miễn phí trên một tuyến bất kỳ.

Bài toán yêu cầu tính chi phí ít nhất mà An phải trả để đi từ ~ 1 ~ đến ~ n ~ khi sử dụng vé miễn phí một lần.

Dữ liệu vào

1. Dòng đầu tiên chứa hai số nguyên ~ n, m ~ (~ 3 \leq n \leq 5000, m \leq 30000 ~): Số nút giao thông và số tuyến xe buýt.
2. ~ m ~ dòng tiếp theo, mỗi dòng chứa ba số ~ i, j, t_{ij} ~ (~ 1 \leq i, j \leq n, 0 \leq t_{ij} \leq 30000 ~):
   • ~ i, j ~: Hai nút giao thông được kết nối bởi tuyến xe buýt.
   • ~ t_{ij} ~: Giá vé của tuyến xe buýt từ ~ i ~ đến ~ j ~.

Dữ liệu đảm bảo luôn có đường đi từ ~ 1 ~ đến ~ n ~.

Dữ liệu ra

• Một số duy nhất là chi phí ít nhất để đi từ nhà An (nút ~ 1 ~) đến trường (nút ~ n ~) khi sử dụng vé miễn phí.

Ví dụ

Input

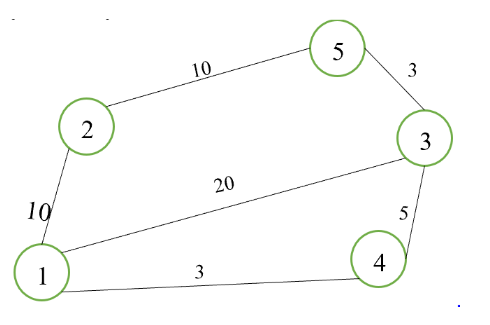
5 6
1 2 10
2 5 10
1 4 3
3 4 5
3 5 3
1 3 20

Output

3

Giải thích

• Đường đi tốt nhất: ~ 1 \to 3 \to 5 ~, sử dụng vé miễn phí trên tuyến ~ 3 \to 5 ~, tổng chi phí là ~ 3 ~.